[4.2]Greedy Algorithm - Shortest Path & MST

在[4-1]Greedy Algorithm - Analysis之後，我們要來看經典的應用Shortest Path 和 Minimum Spanning Tree。

Shortest Path

要找到任意單一點s到其他所有點的最短路徑。

設計演算法

維持一集合S儲存"我們已經決定可從s到達的最短路徑的點"，稱這部分為圖G中"explored"的部分。最初S={s}且d(s)=0。接者我們對V-S當中每一點去找可由S中的點所連接起來的最短路徑。

Dijkstra's Algorithm

Dijkstra's Algorithm （G,l）
Let S be the set of explored nodes
    For each u∈S, we store a distance d(u)
Initially S={s} and d(s)=0
While S ≠ V
    Select a node v ∉ S with at least one edge from S for which d(v)′=MINe=(u,v):u∈s d(u)+le is as small as possible
    Add v to S and define d(v)=d′(v)
EndWhile

分析演算法

定理1

考慮集合S在演算法執行中的任一階段。對於每個S中的元素u，path Pu是最短的s-u路徑。

證明

以歸納法，當|S|=1時肯定為真。假設當|S|=k時的情況，K>=1也為真。現在將|S|變為k+1，藉由加入點v，且(u,v)是s-v路徑Pv的最後一邊。

根據歸納法的假設，Pu是s-v的最短路徑，其中u屬於S。現在考慮另外一條s-v路徑P，我們希望可以證明其至少跟我們的路徑Pv一樣長。

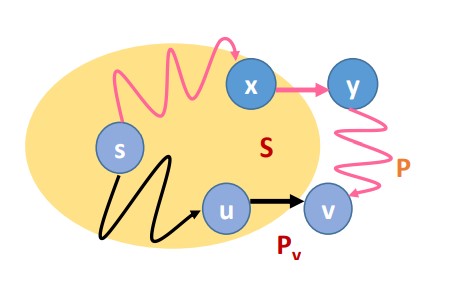
為了到達v，P路徑一定會在某一地方離開集合S，令y為離開S後的第一個點，而x是y前面的一點且屬於S。P不可能比Pv還短，因為在離開S時，P就已經至少和Pv一樣長 : 在這第k+1迴圈中，Dijkstra 演算法肯定有考慮將y加入S（透過x），但其拒絕了這個選擇而加入了v，代表路徑P(s-x-y)一定大於路徑Pv(s-u-v)

另一證明

P'是s-x的子路徑，因為x屬於S，所以根據假設Px是到x的最短路徑（路徑長為d(x)），得到 l(p') > l(px) =d(x)，所以經由P至y的路徑長為 : l(p') + l(x,y) > d(x)+l(x,y) >= d'(y)，且完整路徑P至少和這一路徑一樣長。最後，因為該演算法在這一回合是挑選v，代表d'(y) >= d'(v) = l(Pv)。綜合上述，可得l(P) >= l(p')+l(x,y) >= l(Pv)

兩個觀察

1. 當有邊上的路徑長度為負值時，該演算法無法找到最短路徑

2. 該演算法其實比上面敘述的更簡單，可以說是 持續地 執行BFS

   像是水在水管中依序流到游進到遠的節點

實行與時間複雜度

對於有n個點的圖來說，while loop會執行n-1次，每一次都會加入一點v到S，如何選擇v是相對需要投入心力的部分。從演算法直接來看的話，我們每次要加入點v（v不屬於S）會需要找從S到v的所有邊長，若圖形G有m條邊，那麼這步驟就需要O(m)，整個執行完就是O(mn)。

更好的資料結構

上面步驟可能會讓執行時間很長，我們可以建立Min Heap來免去每次需要再掃描每條邊的動作，因此，時間複雜度會變成 O(m)+取出最小值並回復成heap的時間 = O(mlogn)

MST

問題 : 一地點集合V = {v1,v2,...vn}要讓集合內每一點相通。

定理4.16

T是我們找到的最小成本的解，那麼（V , T）必定為一棵樹。

證明

根據定義 （V , T）一定相連connected，我們要證明他也必定不含cycle。

假設含有一cycle C，而e是C當中的一個邊。我們宣稱(V , T-{e})仍舊connected，因為之前通過e的路徑可以"繞遠路"以C的另一條邊到達目的地。那麼也就是說(V , T-{e})也是一個合理的解，而且因為少了e，成本又更小了，和假設矛盾（T是最小成本的解）

若我們允許一些邊的cost=0的話，也就是說我們只限定Ce是非負的，那麼這組求出來有最小成本的解可能包含許多額外的邊－這些cost=0的邊可以被刪除。僅管有這樣的情形，我們依舊總是可以找到有最小成本的解是一棵樹。

若（V , T）是一棵樹，我們稱這個子集合T⊆E是G的spanning tree，而根據上面定理4.16又可知道我們找到的是圖中最小成本的樹，因此又可稱為Minimum Spanning Tree。除非G是非常簡單（simple）的樹，否則通常會有非常多不同的解集合。

設計演算法

下面介紹三種貪婪演算法

1. Kruskal's Algorithm

   從最小成本的邊開始，依序加入成本再大一些的邊，再加入時考慮加入邊e時會不會造成迴圈，若會的話則捨棄e，再找下一個邊。

2. Prim's Algorithm

   有點像前面用Dijkstra's Algorithm找最短路徑。我們從任一點s開始，貪婪地希望從s長出一棵樹。在每一步，我們加入從現有的樹當中，能夠以最小成本所連接到的點。

   更具體地說，我們維持一集合S⊆V來存放目前為所建立的spanning tree。最初，S={s}，在每一迴圈，加入一點v到S中，其中v擁有最小的"附加成本（attachment cost）"MINe=(u,v):u∈S Ce,，也將邊e加入spanning tree。

3. Reverse-Delete Algorithm

   像是使用"倒轉過來的（backward）或是說"Kruskal's Algorithm。初始狀態是一完整的G=（V , E），並開始以大到小的方式選取邊去做刪除的動作。

分析演算法 - 性質

上面的演算法都需要重複地進行"插入"及"刪除"的動作，所以要分析他們的話，可以從知道 甚麼狀況下進行這些動作是安全的。我們先採用簡化的方式，假設 : 所有邊的成本都是獨一無二的，之後再討論如何將這個假設拿掉。

When is it safe to include an Edge in the MST？

定理4.17 Cut property

假設所有邊的成本都是獨一無二的。令S為是點的子集合，且S非空集合也不包含整個點集合V，令邊e=（v,w）的兩端點連接S及V-S且是最小成本的邊。那麼每一個MST包含邊e。

證明

令T為一不包含e的ST（spanning tree），我們要證明T並非擁有最小可能的成本。以exchange argument來執行 : 我們會在T找到一邊e'的成本大於e，且有辦法在其他ST中將e'換成e，因此這樣就可以如我們所願使得ST總成本就會小於T。

重新回憶一下，e的兩端是點v及w，T是一棵ST，所以T當中必定存在一路徑P可從v到w。從v開始，遵循path，P存在一點w'屬於V-S。令v'屬於S是路徑P上w'的前一點，e' = （v' , w'），可得e'是T中的一條邊且一端在S一端在V-S。接者用e替換掉e'，得到T' = T - {e'} + {e}，再證明T'仍是一棵MST：

• （V,T'）肯定相連connected

  （V,T）是相連的，任何（V,T）中使用e'的路徑在（V,T'）可以被重新導向使用v' , v , (v,w) , w , w'

• （V,T'）沒有cycle

  在（V,T'+{e'}）中唯一的cycle是e和path P

e'一端點在S,一端點在V-S，而e也是，且e成本較低。所以最後可知T'的總成本小於T。

When can we guarantee an Edge is not in the MST？

定理4.20 Cycle property

假設所有邊的成本都是獨一無二的。C是G當中的一cycle，e是C中成本最高的邊。那麼e不屬於MST。

證明

令T為一包含e的ST（spanning tree），我們要證明T並非擁有最小可能的成本。以exchange argument來執行 : 用成本更低的邊來換掉e。

把T中的e刪除，使得其變成兩個components : S含有點v, V-S含有點w。所以我們想用來替換e的邊會連接兩個component，使其重新變回一棵樹。根據定義，C中除了e之外的另一條邊也有一條路徑P可從v到w，所以用存在一條邊e'可連接S和V-S，T' = T - {e} + {e'}，（V,T'）是相連且沒有cycle的，另外在成本方面e>e'，所以T'<T。

Sum up

事實上，任何產生spanning tree的演算法，只要是以 重複加入邊 （在cut property確保正確性之下）以及　重複刪除邊（在cycle property確保正確性之下）這兩種特性產生的，都會是MST。

分析演算法 - 正確性

The Optimality of Kruskal’s Algorithms

重點是 : 這兩個演算法只會在合理的時候加入新的邊（cut property）

定理4.18

Kruskal’s Algorithms 會產生G的MST。

證明

考慮任何被此演算法加入的邊e = (v,w) ，讓集合S是在e被加入之前v有一條路徑P上的所有點集合。因為加入e也不會形成cycle，所以代表v屬於S且w不屬於S。此外，目前尚未有S到V-S的邊，因為那樣的邊可以被加入且不造成cycle，那麼應該已經被加入了。所以e是成本最低的邊，且連接S和V-S，根據cut property，e屬於任何MST。

所以如果我們可以顯示輸出結果（V,T）是G的ST，就完成證明了。首先因為演算法的設計，所以（V,T）沒有cycle。（V,T）是否會不connected？不。（V,T）不connected就代表會被分成至少兩個components S和V-S，且沒有edge可與他們相連，而這違法演算法的設計：因為G是connected，至少會有一條邊連接他們，當遇到時演算法會將此邊加入。

The Optimality of Prim’s Algorithms

定理4.10

Prim’s Algorithms 會產生G的MST。

證明

我們將此演算法找到的解稱為S。用反證法，先假設S不是最小成本，令ES={e1,e2,...,en-1}為演算法產生的邊。U為MST，該MST含有數條邊，為ES序列前最長可能集合（it's a longest prefix of ES）。ei = {x,y}是演算法中第一條不屬於U被加入S的邊，讓W是點集合在ei加入之前，也代表U包含邊e1,e2,...,ei-1，但不包含ei。

在U當中必定存在一path使得x可到y，所以讓(a,b)是這條路徑上的第一條邊，其中a在W，b在W之外，如下圖

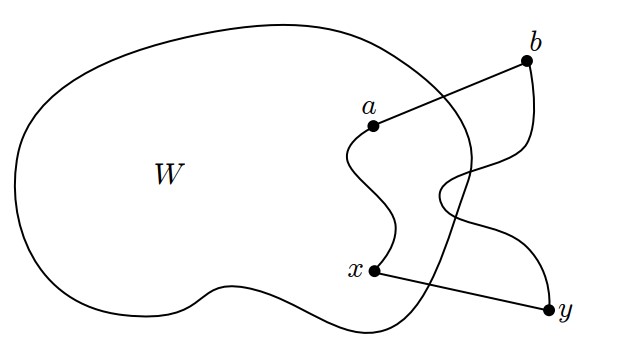
定義T = U + {x,y} - {a,b}，且T是G的ST，對 {x, y} 、{a, b}這兩條邊的成本考慮下面三種可能的情形：

1. w({x, y}) > w({a, b})

   {a,b}成本較小，所以演算法在此步驟應會選擇{a,b}，違反{x,y}的假設。

2. w({x, y}) = w({a, b})

   W(T) = W(U)，所以T也是MST。此外，演算法尚未選到邊{a,b}，這條邊不會是e1,e2,...,ei-1的其中一個，代表T包含e1,e2,...,ei，是一條比U還長的組合，違反tree U的定義。

3. w({x, y}) < w({a, b})

   加入了成本較小的邊，W(T) < W(U)，但這不可能，因為U是MST。

因為所有可能的情況都會造成矛盾，所以可知原始假設S非MST是錯誤的。

The Optimality of Reverse-Delete Algorithm

定理4.21

Reverse-Delete Algorithms 會產生G的MST。

證明

考慮一條被此演算法移除的邊e = {v,w}，在他被移除的時候，他是存在Cycle C當中的。因為他是被演算法移除的邊，代表他是當下所有選擇中成本最高的邊，根據Cycle property，這條邊必定不屬於任何MST。

所以我們只要證明Reverse-Delete的輸出（V , T）是G的ST就完成了。首先（V , T）是connected，因為演算法不會刪除邊使得G變成disconnected。另外用反證法證明（V , T）不含cycle。假設（V , T）含有cycle C，考慮C上成本最高的邊e，這條邊是演算法碰到的第一個碰到的情形，這條邊應該被移除，因為不會造成圖G變成disconnected，這樣違反了Reverse-Delete的行為。

Sum up

最後我們要來消除 所有邊的成本都是獨一無二的這個假設。

有一個簡單的方法就是：將每一條邊的成本都加上一些不同的極小數字，讓他們可以變得獨一無二。現在原先有的邊的成本排序並不會被打亂，因為加入的成本非常非常小，只是足以讓有相同成本的邊變得有一點點不同。

實行Prim's Algorithm

如果有好的資料結構可以是O(mlogn)。

雖然證明正確性的方式和Dijkstra's 差很多，但是在實行上基本是相同的。我們一樣要決定哪一點應該被加入S當中，所以也是利用priority queue，共執行n-1次迴圈，每一回都都取出最小的並維持queue得正確性。 O(m)+取出最小值並回復成heap的時間 = O(mlogn)

實行Kruskal's Algorithm : The Union-Find Data Structure

在[3]Graph時有用過BFS、DFS都可以幫我們找到G的connected components。在Kruskal's Algorithm中會有些不同，因為我們會"動態"增加新的點到G當中，我們並不會希望每次都需要重新計算，因此我們需要使用叫做 Union-Find的資料結構。簡單來說，當我們要將e=(v,w)加入S時，需要辨認v和w是否已有相連，暫且稱v和w都有其"身分認證"，若兩者身分相同代表已相連，則不加入e；若兩者身分不同，則將e加入。另外，加入後還需要有快速地方法將v和w的身分認證更新為相同的。其中，確認身分的行為稱為 Find；更新身分稱為 Union。

• MakeUnionFind(S) : 對集合S使用，回傳給我們Union-Find的資料結構，也就是說S當中的每一元素都被劃分成一個只包含自己的集合。這一步希望可以在O(n)的時間內完成，n=|S|。
• 對於S當中每一元素u，Find(u)會回傳包含u的這一集合的名稱。希望是O(logn)，甚至可以是O(1)。
• 對於兩集合A、B，Union(A,B)會改變資料結構 : 合併集合AB成為單一集合。希望是O(logn)。

A simple Data Structure

一個可能是最簡單的方式 : 用一陣列儲存。

S={1,2,...,n}是有n個元素的集合，設定一陣列 Component[n]，而component[s]就是含有s的集合的名稱。

• MakeUnionFind(S)

  初始化一陣列，其中對於所有屬於S的s，component[s] = s 。

• Find(s)

  O(1)

• Union(A,B)

  至多需要O(n)，因為我們要去改集合A、B中所有元素s的component[s]的值。

Union這一步驟可以做一些改善，例如其實我們只需要改A或B其中一個的components的值，其中，又可以去記錄說集合A、B哪一個擁有的元素較少，這樣改起來比較有效率，但最差的情況仍有可能是O(n)，不過這並不常發生，所以我們想要更精確地去描述所需要的時間。與其用the worst-case去界定 單一是Union operation 的執行時間的上限，我們以 一執行k次Union operations程序的總時間（或平均）。

定理4.23

考慮大小為n的集合S是一用陣列執行Union-Find的資料結構，且unions使用較大的集合作為名稱。MakeUnionFind需要O(n)；Find需要O(1)；任一執行k次Union operations的程序至多需要O(klogk)的時間。

證明

再提一次，一開始我們將S中n個元素都分為只包含自己的集合（因此共n個集合）。一次的Union動作至多牽涉2個這些原本只包含一元素的集合，所以在執行任k次Union程序後，至多2k個元素完全沒有被動過。現在考慮一特別的元素v，當v的集合參與了Union後，集合一定會變大。在Union時，一定有時候component[v]的值會被新，有些時候不會。但依據我們的慣例，使用較大的集合之名稱去做更改，所以每次更新component[v]時，擁有v的集合的大小會至少變為兩倍。集合v大小從1開始，最大為2k（因為前面所說至多剩下2k個完全沒動過的元素）。因此component[v]至多更新log(2K)次（log底數為2）在整個過程中。另外，至多2K個元素參與Union。所以得到上界為O(klogk)。

這樣的平均值行時間對於許多應用已經可以接受，但是我們可以試著改善，減少worst-case發生時會需要那麼多時間的成本，此方法也相對會需要提升Find到O(logn)。

A Better Data Structure

使用指標（pointer），每一點都會有依靠指標指到自己的集合紀錄。

• MakeUnionFind(S):

  將S內各元素u的指標指向自己（也就是目前他們屬於自己這個集合）。

• Union :

  Union by rank : 用較小的tree去接較大的tree，如此一來會比較扁平，比較容易找到要找的元素

  

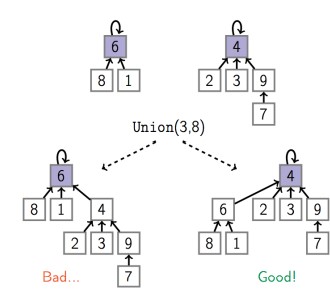
• Find:

  path compression : 指的是如下圖，當我們在find(6)=5後，讓從6找到5時所經過的所有點也都直接指向5，也可以讓結構變得更扁平。

  

實行Kruskal's Algorithm

如果有好的資料結構可以是O(mlogn)。

Kruskal's (G,c)
1.{e1,e2,...,em}=sorted edges in ascending order
2.T=∅
3.For each ei = (u,v)
4.  if(u and v are not connected by edges in T)
5.      T=T+{ei}

使用 UnionFind

• 將每一connected component維持為一不相交的集合（disjoint set）

• Line1 : Sort edge cost

  需要O(mlogm)，因為兩點間至多就一條邊，因此m≦n^2，所以也可說是O(mlogn)

• Line4 : 查看Find(u)和Find(v)是否相異，代表可以合併。（至多2m次）

• Line5: Union(u,v) （至多n-1次）

時間複雜度 O(mlogn)